Uso de pilas en la recursión, pseudocodigo para calcular factorial

Hola queridos lectores, como ya estuvo bien de tanta weba hoy aportare algo a la comunidad a peticion del publico. Como es que se aplican las pilas en problemas de recursion (al menos asi lo entendi en los comentarios).

Bueno para lograr este cometido vamos a definir lo que es recursion y pilas de una manera breve, si quuieren profundizar mas, deberán leer post anteriores.

Definición formal

Recursión.-(Segun wikipedia) es la forma en la cual se especifica un proceso basado en su propia definición.

Yo diría que la recursión se hace presente cuando, un proceso definido para darle solucion a un problema tenga que llamarse a si mismo 1 o varias veces para lograr su cometido. Hay muchos ejemplos de recursión. En esta ocasion lo representare con la siguiente imagen:

Bueno, esperando que ya se tenga mas clara la idea de recursión, continuaremos con la definición de pila.

Pila: Es una lista de elementos a la cual se le pueden insertar y retirar elementos solo por uno de los extremos. En consecuencia, los elementos de una pila seran retirados en orden inverso al que se insertaron. Ver detalle…

Pues bien, ahora lo que sigue es dar un ejemplo de como es que se fusionan estos dos conceptos.

Fusión

No me quebrare la cabeza y pondré un ejemplo típico de recursividad. Imaginemos que tenemos que calcular la siguiente operación: 6! (este es un numero factorial, para los que no están enterados, este numero se calcula así: 6*5*4*3*2*1=720, entonces 6!=720)

Suponiendo que tenemos el siguiente método que resuelve el problema:

Algoritmo

factorial( n )

si n=0 entonces

return 1; //estado básico del método recursivo

si no

return n*factorial(n-1); //llamada recursiva

Fin // si n=0

Fin //del método

Explicación

Pero que pasa cuando se llama el metodo a si mismo? que pasa con las variables?. Aqui es donde entran en accion las pilas. Estos valores son guardados en pilas para poder ser recuperados posteriormente de tal manera que no se altere el producto. Para expliar mejor eso, vamos la siguiete tabla:

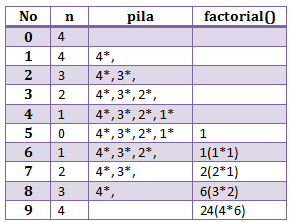
En el primer paso n es igual a 4, por lo tanto siguiendo el algoritmo debe hacerse 4*3!, pero no puede realizarse la operación por que 3! no ha sido calculado. Así que hay que guardar el valor de n en la pila para calcular con el mismo algoritmo factorial el valor de 3!. Ahora continuamos trabajando con n=3. Tenemos otra vez la misma situación, el algoritmo quiere hacer la operación 3*2!, pero 2! no esta calculado aun, así que de nuevo guardamos el valor de n en la pila y continuamos con n=2. Esto se repetirá hasta que el método llegue a su estado básico, cuando esto suceda, el método factorial por fin arrojará un valor y se podrán empezar a calcular todos los valores que esperan en la pila. En el paso 6 extraemos el valor 1 de la pila y lo multiplicamos por el factorial de 0, de esta operación resulta 1. Se saca el 2 de la pila y se multiplica por el factorial de 1! recién calculado (!0*1=1!), se obtiene el factorial de 2! (!1*2=!2), y asi sucesivamente hasta obtener el !4. Espero aclarar su mente con la siguiente figurilla:

Ojalá que esta explicación macabra les sea de utilidad. Mucha suerte en todo.

Fin